Computación ET-344
Perfilado de sección
-
 Profesores:
Profesores:- Ing. Daniel Refosco
- Ing. Germán Xander
- Ing. Gerardo Mathias Iurinic.
Este curso es para los alumnos de 3er año de la Carrera de Ingeniería Electrónica de la Facultad de Ingeniería. Se dicta en el 1er cuatrimestre. -
-
Horarios y Aulas.
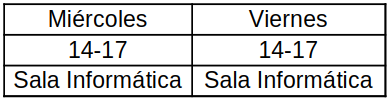
-
426.2 KB
-
Foro Profesores
-
-
-
36.0 KB
-
678.2 KB
-
Efecto 1 Archivo AVI1.1 MB
-
3.8 MB
-
894.2 KB
-
734.5 KB
