Computación ET-344
Contorno da seção
-
 Profesores:
Profesores:- Ing. Daniel Refosco
- Ing. Germán Xander
- Ing. Gerardo Mathias Iurinic.
Este curso es para los alumnos de 3er año de la Carrera de Ingeniería Electrónica de la Facultad de Ingeniería. Se dicta en el 1er cuatrimestre. -
-
Horarios y Aulas.
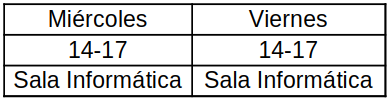
-
426.2 Kb
-
Foro Profesores Fórum
-
-
-
36.0 Kb
-
678.2 Kb
-
Efecto 1 Arquivo AVI1.1 Mb
-
3.8 Mb
-
894.2 Kb
-
734.5 Kb
-
-
Final 25/02/2026 Tarefa
Sistema de registro de sensores ambientales (industria / IoT)
Contexto:
Una empresa de automatización industrial instala nodos de monitoreo ambiental en distintas salas de una planta. Cada nodo registra información básica tomada manualmente por un operador, ya que la adquisición automática y almacenamiento en una base de datos aún no está implementado.
Cada registro contiene 4 valores:
-
ID del sensor
-
Temperatura medida (°C)
-
Humedad relativa (%)
-
Cantidad de lecturas realizadas
Los datos se cargan en un software desarrollado en C++, que el alumno debe desarrollar.
en C++ y que permita gestionar los registros utilizando una lista enlazada simple.
La estructura de datos es global, y una clase con sus métodos se encarga de realizar las operaciones.El programa debe mostrar un menú con las siguientes opciones:
-
Cargar n registros de sensores (alta n registros)
-
Calcular la cantidad total de lecturas de un sensor dado su ID
-
Eliminar el primer sensor cuya temperatura sea menor a un valor dado
-
Listar todos los sensores cargados.
-
Salir
Consideraciones:
-
Validar que
ndebe ser mayor que cero. -
ID del sensor: entero en el rango [500, 1500] .
-
Temperatura: valor real en el rango [-10.0 , 50.0].
-
Humedad: valor real en el rango [0.0 , 100.0]
-
Cantidad de lecturas: entero positivo
- En caso que el ingreso NO sea válido en el rango respectivo se debe solicitar reingreso
-
-
