Computación ET-344

Trataremos sobre uno de los problemas más vastos de la aproximación numérica la solución de ecuaciones no lineales analizado de diferentes maneras desde la óptica analítica y su interpretación geométrica.
En el campo de la tecnología principalmente en la ingeniería nos encontramos generalmente  con el siguiente problema  determinar las raíces de la ecuación f(x) = 0.
Como la teoría de la difracción de la luz se precisa de la siguiente función:

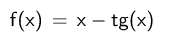
Su gráfica es:

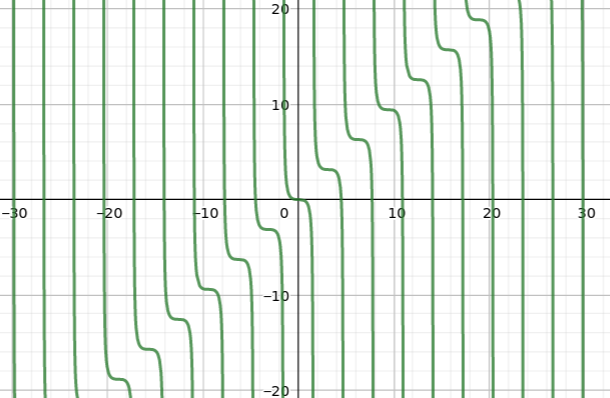
Otra podría ser la expresión para determinar las orbitas planetarias se precisa de la ecuación llamada ecuación de Kepler:

x- a. sen(x) =b

con a y b tomando diversos valores.

Es decir f(x) puede ser una función de variable real x, como es un polinomio en x, o como una función trascendente es decir:

O una función trascendente  ( Una función trascendente es una función que no satisface una ecuación polinómica cuyos coeficientes sean a su vez polinomios)

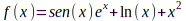
Para dar solución a estos problemas existen distintos algoritmos o métodos para encontrar las raíces de f(x) = 0, pero debemos tener en cuenta que ninguno es general, pues   en otras palabras no existe un método que funcione con todas las ecuaciones perfectamente.
Pero sólo en un reducido caso será posible obtener  las raíces  exactas de f(x) = 0, es decir cuando se trata de f(x)  factorizable,  en tal sentido tenemos:

donde  r_i son las raices.

El método de punto fijo o de aproximaciones sucesivas es, junto con el de Bisección, uno de los primeros métodos que se utilizaron para resolver ecuaciones algebraicas y trascendentes. No obstante que en la actualidad existen otros métodos más eficientes, el de punto fijo se considera el más simple en sus principios y en él se pueden apreciar claramente todas las características de un método de aproximaciones sucesivas.