Introducción a Redes

Se presenta un parámetro relacionado con la SNR que es más adecuado para determinar las tasas de error y la velocidad de transmisión.
Se usa habitualmente para medir la calidad de las prestaciones de los sistemas de comunicación digital.
Este parámetro es el cociente de la energía de la señal por bit entre la densidad de potencia del ruido por hercio:   $\frac{E_b}{N_0}$
Cuanto mayor sea el cociente, quiere decir que el bit tiene mayor energía que el ruido.
Sea una señal, digital o analógica, que contenga datos digitales binarios transmitidos a una determinada velocidad R. Teniendo en cuenta que $1 \, \text{W} = 1 \, \text{J/s}$, la energía por bit de la señal será $E_b = S \cdot T_b$ , donde S es la potencia de la señal y $T_b$ es el tiempo necesario para transmitir un bit.
La velocidad de transmisión es $R = \frac{1}{T_b}$  . Por tanto:
$\frac{E_b}{N_0} = \frac{\frac{S}{R}}{N_0} = \frac{S}{kT R}$
Nótese que cuando se aumenta la velocidad de transmisión R, la potencia de la señal transmitida S, , debe aumentarse para mantener el cociente $\frac{E_b}{N_0}$ en el nivel deseado.
Para ruido termico Blanco : 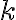$N_0 = kT$, $k$ = Boltzman’s constant ($N_0 = (1.38 \times 10^{-23}) \cdot T$) y $T = 290 \, \text{K}$ para Temp. Ambiente.