Imprimir el Libro CompletoImprimir el Libro Completo

Introducción a Redes

Sitio: Facultad de Ingeniería U.Na.M.
Curso: REDES I - IC412
Libro: Introducción a Redes
Imprimido por: Invitado
Día: miércoles, 4 de diciembre de 2024, 23:02

Tabla de contenidos

1. Transmisión de Datos

Cuestiones Básicas.

La mayoría de las imágenes publicadas en la presentación pertenecen a:

Stallings, William.Data and computer communications/William Stallings.—Tenth edition

1) Todos los tipos de información considerados en este texto (voz, datos, imágenes, vídeo) se pueden  representar mediante señales electromagnéticas. Para transportar la información, dependiendo del medio de transmisión y del entorno donde se realicen las comunicaciones, se podrán utilizar señales analógicas o digitales.


2) Cualquier señal electromagnética, analógica o digital, está formada por una serie de frecuencias constituyentes. Un parámetro clave en la caracterización de la señal es el ancho de banda, definido como el rango de frecuencias contenidas en la señal. En términos generales, cuanto mayor es el ancho de banda de la señal, mayor es su capacidad de transportar información.

3) Uno de los problemas principales en el diseño de un sistema de comunicaciones reside en minimizar las dificultades, o defectos, de las líneas de transmisión. Las dificultades más importantes a superar son

  • la distorsión 
    • por atenuación
    • por retardo
  • los distintos tipos de ruido. 
    • térmico
    • intermodulación
    • diafonía
    • impulsivo

Al usar señales analógicas, las dificultades en la transmisión causan efectos de naturaleza aleatoria que degradan la calidad de la información recibida y pueden afectar a la inteligibilidad. 

Cuando se utilizan señales digitales, los defectos en la transmisión pueden introducir bits erróneos en la recepción.

4) El diseñador de un sistema de comunicaciones debe tener presente cuatro factores determinantes todos relacionados

  1. el ancho de banda de la señal,
  2. velocidad de transmisión de la información digital,
  3. cantidad de ruido, además de otros defectos en la transmisión.
  4. la proporción o tasa de errores tolerable.

El ancho de banda disponible está limitado por el medio de transmisión así como por la necesidad de evitar interferencias con señales cercanas. Debido a que el ancho de banda es un recurso escaso, es conveniente hacer máxima la velocidad de transmisión para el ancho de banda disponible.

La velocidad de transmisión está limitada por el ancho de banda, por la presencia ineludible de defectos en la transmisión, como el ruido, y, finalmente, por la tasa de errores que sea tolerable.


1.1. Conceptos y Términos


Medios Guiados

En los medios guiados, por ejemplo en pares trenzados, en cables coaxiales y en fibras ópticas, las ondas se transmiten confinándolas a lo largo de un camino físico

Medios No Guiados

los medios no guiados, también denominados inalámbricos, proporcionan un medio para transmitir las ondas electromagnéticas sin confinarlas, como por ejemplo en la propagación a través del aire, el mar o el vacío.

Enlace Directo

El término enlace directo se usa para designar un camino de transmisión entre dos dispositivos en el que la señal se propague directamente del emisor al receptor sin ningún otro dispositivo intermedio que no sea un amplificador o repetidor. 

Punto a Punto

Un medio de transmisión guiado es punto a punto si proporciona un enlace directo entre dos dispositivos que comparten el medio, no existiendo  ningún otro dispositivo conectado. Ver que aquí no se menciona Repetidor o Amplificador

Multipunto

En una configuración guiada multipunto, el mismo medio es compartido por más de dos dispositivos.

Simplex

En la transmisión simplex, las señales se transmiten sólo en una única dirección; siendo una estación la emisora y otra la
receptora.

Half Duplex

En half-duplex, ambas estaciones pueden transmitir, pero no simultáneamente.

  ó 

Full Duplex

En full-duplex, ambas estaciones pueden igualmente transmitir y recibir, pero ahora simultáneamente. En este último caso, el medio transporta señales en ambos sentidos al mismo tiempo.

FRECUENCIA, ESPECTRO Y ANCHO DE BANDA

 Figura 1

En el  punto que indica la flecha tendremos los conceptos de:

  • Frecuencia
  • Espectro 
  • Ancho de Banda

Señal Digital

Señal digital es aquella en la que la intensidad se mantiene constante durante un determinado intervalo de tiempo, tras el cual la señal cambia a otro valor constante. En la Figura 1 ( g(t) y g'(t) ) se muestran ejemplos de ambos tipos de señales. La señal continua puede corresponder a voz y la señal discreta puede representar valores binarios (0 y 1).

Señales Periódicas

señales periódicas son el tipo de señales más sencillas que se puede considerar; se caracterizan por contener un patrón que se repite a lo largo del tiempo. Matemáticamente, una señal s(t) se dice periódica si y solamente si:

Estas señales periódicas se pueden representar matemáticamente  por una serie de Fourier que constituyen la herramienta matemática básica del análisis y que consiste en la descomposición de dicha función periódica en una suma infinita de funciones sinusoidales mucho más simples (como combinación de senos y cosenos con frecuencias enteras).

Señal No periódica.

En cualquier otro caso la señal no es periódica.

Figura 2

Sería una señal analógica y no periódica.

 Figura 3

Sería una señal digital no periódica

Longitud de Onda.

Se define como Longitud de onda,  la distancia que ocupa un ciclo o, en otras palabras, se define como la distancia entre dos puntos de igual fase en dos ciclos consecutivos, esto por supuesto es para ondas periódicas.

Frecuencia Fundamental.

Cuando todas las componentes de una señal tienen frecuencias múltiplo de una dada, esta  última se denomina frecuencia fundamental, esto es fácil de ver en una onda cuadrada.

Armónico.

Un armónico de una onda es un componente sinusoidal de una señal, esto es fácil de ver en una onda cuadrada

Fourier.

Según Fourier, que cualquier señal está constituida por componentes sinusoidales de distintas frecuencias. Sumando un número suficiente de señales sinusoidales, cada una con su correspondiente amplitud, frecuencia y fase, se puede construir cualquier señal
electromagnética. En otras palabras, se puede demostrar cualquier señal electromagnética que está constituida por una colección de señales periódicas analógicas (ondas seno) con diferentes amplitudes, frecuencias y fases. Veamos en el domínio tiempo.

Figura 4

Veamos un ejemplo con  Python y Fourier vamos a mostrar gráficas de 5 , 10 y 50 armónicos para ver como se aproxima a la onda cuadrada..

5 Armónicos.

10 Armónicos.

50 Armónicos.

Si continuamos sumando infinitos armónicos impares podríamos lograr una onda cuadrada perfecta:

Figura 5

En el dominio de la Frecuencia esto ser vería de la siguiente manera:

Figura 6

Espectro.

Se define el espectro de una señal como todo el conjunto de frecuencias que la constituyen

Ancho de banda efectivo.

La mayor parte de la energía de la señal se concentra en una banda de frecuencias relativamente estrecha. Esta banda se denomina ancho de banda efectivo o, simplemente, ancho de banda. Si lo pensamos en términos de conjunto y sub-conjunto:


1.2. Relación Ancho de Banda Velocidad de Transmisión


Vamos a fijar el concepto de la relación entre al Ancho de banda de un canal y la velocidad de transferencia de un canal.

Imaginemos una onda cuadrada de una frecuencia de 2 Hz., si el pulso positivo es un uno y el negativo un cero. podemos decir:

1 Hz => 2 bits / Segundo ó 2 bps.


Haciendo un razonamiento extensivo

1000 Hz => 2000 bps

10 MHz => 20 Mbps.

En esta suposición los "datos" son en realidad una onda cuadrada periódica.. algo que en realidad difícilmente exista como dato.

Conclusión de hacer un razonamiento extensivo es que cuando mayor es el Ancho de banda , mayor podría ser la velocidad de transmisión.

En la Figura 1 se muestra una cadena de bits con una velocidad de transmisión de 2.000 bits por segundo. Con un ancho de banda igual a 2.500 Hz, o incluso 1.700 Hz, la representación es bastante buena. Es más, estos resultados son generalizables de la siguiente manera. Si la velocidad de transmisión de la señal digital es W bps, entonces se puede obtener una representación muy buena con un ancho de banda de 2W Hz. No obstante, a menos que el ruido sea muy elevado, la secuencia de bits se puede recuperar con un ancho de banda menor

 Figura 1

Esto permite fijar el concepto sobre la estrecha relación entre la forma de la onda, el ancho de banda y la velocidad


1.3. Dato, Información, Señal

Dato.

se define dato como cualquier entidad capaz de transportar información. Las señales son representaciones eléctricas o electromagnéticas de los datos, no hay unidades, son solo números.

Información (= dato + procesamiento).

Lo que hace la diferencia entre Datos e Información es el Procesador ( persona o máquina )

Entonces podemos decir que "la información es el conocimiento producido como resultado del procesamiento de los datos."

Aquí un número puede tener unidades dependiendo de que representa, temperatura, longitud, velocidad.

Señal

Las  señales son representaciones eléctricas o electromagnéticas de los datos.

Señalización.

La señalización es el hecho de la propagación física de las señales a través de un medio adecuado.

Pregunta para el alumno: ¿Todos los armónicos viajan a la misma velocidad?

Transmisión.

Se define transmisión como la comunicación de datos mediante la propagación y el procesamiento de señales.


2. Dificultades en las Transmisiones

.

2.1. Distorsión por retardo

Distorsión por Retardo

La distorsión de retardo es un fenómeno debido a que la velocidad de propagación de una señal a través de un medio guiado varía con la frecuencia. Para una señal limitada en banda, la velocidad tiende a ser mayor cerca de la frecuencia central y disminuye al acercarse a los extremos de la banda. Por tanto, las distintas componentes en frecuencia de la señal llegarán al receptor en instantes diferentes de tiempo, dando lugar a desplazamientos de fase entre las diferentes frecuencias.
Este efecto se llama distorsión de retardo, ya que la señal recibida está distorsionada debido al retardo variable que sufren sus componentes. La distorsión de retardo es particularmente crítica en la transmisión de datos digitales.

¿Por que no hay distorsión por retardo en medios NO guiados?

Debido a la poca diferencia que existe entre la velocidad de propagación en el vacío y en el aire, se considera que en el aire también se propagan a una velocidad de 300.000.000 m/s.

1) Las ondas electromagnéticas, como las ondas de radio, luz visible y microondas, se propagan a la velocidad de la luz en el vacío, son velocidades muy altas y esto hace que la diferencia de tiempo con la que llegan las distintas componentes sea mínima.
2) En medios no guiados, como el espacio libre, las ondas electromagnéticas se propagan de manera esférica desde su fuente. A medida que se alejan de la fuente, la energía de la onda se dispersa en un patrón tridimensional. Aunque la intensidad de la señal disminuye con la distancia debido a la expansión de la superficie de la esfera, no se produce distorsión en el tiempo de llegada de la señal.


2.2. RUIDO


Para cualquier dato transmitido, la señal recibida consistirá en la señal transmitida modificada por las distorsiones introducidas en la transmisión, además de señales no deseadas que se insertarán en algún punto entre el emisor y el receptor. A estas últimas señales no deseadas se les denomina ruido. El ruido es el factor de mayor importancia de entre los que limitan las prestaciones de un sistema de comunicación.

La señal de ruido se puede clasificar en cuatro categorías:

  • Ruido térmico.
  • Ruido de intermodulación.
  • Diafonía.
  • Ruido impulsivo.

2.3. Ruido Térmico

El ruido térmico se debe a la agitación térmica de los electrones. Está presente en todos los dispositivos electrónicos y medios de transmisión; como su nombre indica, es función de la temperatura.
El ruido térmico está uniformemente distribuido en el espectro de frecuencias usado en los sistemas de comunicación, es por esto por lo que a veces se denomina ruido blanco. El ruido térmico no se puede eliminar y, por tanto, impone un límite superior en las prestaciones de los sistemas de comunicación. Es especialmente dañino en las comunicaciones satelitales ya que, en estos sistemas, la señal recibida por las estaciones terrestres es muy débil.

En cualquier dispositivo o conductor, la cantidad de ruido térmico presente en un ancho de banda de 1 Hz es :


N0 densidad de potencia del ruido, en vatios por 1 Hz de ancho de banda.
k  constante de Boltzmann % 1,38 x 1023 J/K.
T  temperatura absoluta, en grados Kelvin.

Se supone que el ruido es independiente de la frecuencia. Así pues, el ruido térmico presente en un ancho de banda de B hercios se puede expresar como


2.4. Ruido de Intermodulación

Se produce cuando dos o más señales de diferentes frecuencias se mezclan en un dispositivo no lineal, generando nuevas frecuencias no deseadas. Puede ser un problema en los sistemas de comunicación de alta frecuencia.

Se suele generar por Alinealidades en los sistemas de amplificación.

2.5. Diafonía

La diafonía la ha podido experimentar todo aquel que al usar un teléfono haya oído otra conversación; se trata, en realidad, de un acoplamiento no deseado entre las líneas que transportan las señales. Esto puede ocurrir por el acoplamiento eléctrico entre cables de pares cercanos o, en raras ocasiones, en líneas de cable coaxial que transporten varias señales. La diafonía también puede aparecer cuando las señales no deseadas se captan en las antenas de microondas; aunque éstas se caracterizan por ser altamente direccionales, la energía de las microondas se dispersa durante la transmisión. Generalmente, la diafonía es del mismo orden de magnitud (o inferior) que el ruido térmico.


2.6. Ruido impulsivo


Ruido impulsivo

Generalmente, el ruido impulsivo no tiene mucha transcendencia para los datos analógicos.

Por ejemplo, la transmisión de voz se puede perturbar mediante chasquidos o crujidos cortos, sin que ello implique pérdida significativa de inteligibilidad.

Sin embargo, el ruido impulsivo es una de las fuentes principales de error en la comunicación digital de datos.

Por ejemplo, un pico de energía con duración de 0,01 s no inutilizaría datos de voz, pero podría corromper aproximadamente 560 bits si se transmitieran a 56 kbps


3. Capacidad del Canal

La mayoría de las imágenes publicadas en la presentación pertenecen a:

Stallings, William.Data and computer communications/William Stallings.—Tenth edition y anteriores.

Se denomina capacidad del canal a la velocidad máxima a la que se pueden transmitir los datos en un canal, o ruta de comunicación de datos, bajo unas condiciones dadas.

Hay cuatro conceptos relacionados con esto.

  • La velocidad de transmisión de los datos: velocidad, expresada en bits por segundo (bps), a la que se pueden transmitir los datos.
  • El ancho de banda: ancho de banda de la señal transmitida; éste estará limitado por el transmisor y por la naturaleza del medio de transmisión; se mide en ciclos por segundo o hercios.
  • El ruido: nivel medio de ruido a través del camino de transmisión.
  • La tasa de errores: tasa a la que ocurren los errores. Se considera que ha habido un error cuando se recibe un 1 habiendo transmitido un 0, o se recibe un 0 habiendo transmitido un 1.

3.1. Ancho de Banda de Nyquist


Para comenzar, considérese el caso de un canal exento de ruido. En este entorno, la limitación en la velocidad de los datos está impuesta simplemente por el ancho de banda de la señal. Nyquist formalizó esta limitación, afirmando que si la velocidad de transmisión de la señal es 2B, entonces una señal con frecuencias no superiores a B es suficiente para transportar esta velocidad de transmisión de la señal. Y viceversa: dado un ancho de banda B, la mayor velocidad de transmisión de la señal que se puede conseguir es 2B. Esta limitación está provocada por la interferencia entre símbolos que se produce por la distorsión de retardo. Este resultado es de utilidad en el diseño de convertidores digital a analógico

Si las señales a transmitir son binarias (dos niveles de tensión) pensemos para facilitar el razonamiento en una onda cuadrada, la velocidad de transmisión de datos que se puede conseguir con B Hz es igual a 2B bps.

Figura 1

Supóngase un ancho de banda de 3100 Hz., entonces, la capacidad C del canal es 2B = 6.200 bps.

No obstante, como se verá mas adelante, se pueden usar señales con más de dos niveles; es decir, cada elemento de señal puede representar
a más de dos bits.

Por ejemplo, si se usa una señal con cuatro niveles de tensión, cada elemento de dicha señal podrá representar dos bits. La formulación de Nyquist para el caso de señales multinivel es:

C = 2 \cdot B \cdot \log_2 M = (2 \cdot B \cdot \text{Ncantidad de bits})

donde M es el número de señales discretas o niveles de tensión y B el ancho de banda.

Así pues, para M=8, valor típico que se usa en algunos módem, la capacidad resulta ser 18.600 bps, siendo el ancho de banda igual a 3.100 Hz.

Que consecuencias trae en el diseño electrónico procurar un M grande?

Que consecuencias trae el ruido en un diseño con M grande?

El ruido, aparece en la expresión ?


Observación.

Si tengo N bits, la cantidad de combinación posible es 2N 

O sea que voy a necesitar M niveles de tensión distintos para poder representar N bits, donde M=2N

3.2. Capacidad de Canal según SHANNON

La fórmula de Nyquist implica que al duplicar el ancho de banda se duplica la velocidad de transmisión, si todo lo demás se mantiene inalterado. Ahora establezcamos una relación entre la velocidad de transmisión, el ruido y la tasa de errores, esto hace la expresión de Shannon.

La presencia de ruido puede corromper uno o más bits.

Si se aumenta la velocidad de transmisión, el bit se hace más «corto», de tal manera que dado un patrón de ruido, éste afectará a un mayor número de bits. Así pues, dado un nivel de ruido, cuanto mayor es la velocidad de transmisión, mayor es la tasa de errores.

La relación señal-ruido es importante en la transmisión de datos digitales, ya que ésta determi-
na la máxima velocidad de transmisión que se puede conseguir.

Una conclusión de Shannon es que la capacidad máxima del canal, en bits por segundo, verifica la ecuación:

C = B \cdot \log_2(1 + \text{SNR})

C: Capacidad del Canal

 B:Ancho de Banda.

La fórmula de Shannon representa el máximo límite teórico que se puede conseguir. Sin embargo, en la práctica, se consiguen velocidades mucho menores. Una razón para esto reside en el hecho de que la fórmula anterior supone ruido blanco (ruido térmico) y no se han tenido en cuenta el ruido impulsivo, la distorsión de atenuación o la distorsión de retardo.
La capacidad, tal y como se ha calculado en la fórmula precedente, se denomina capacidad libre de errores

Como puedo mejorar la capacidad del Canal ?

Que consecuencias puede tener incrementar la potencia de la señal?

Que consecuencias tiene el incrementar el ancho de banda respecto de SNR?

3.3. Cociente Eb / No

Se presenta un parámetro relacionado con la SNR que es más adecuado para determinar las tasas de error y la velocidad de transmisión.
Se usa habitualmente para medir la calidad de las prestaciones de los sistemas de comunicación digital.
Este parámetro es el cociente de la energía de la señal por bit entre la densidad de potencia del ruido por hercio:   \frac{E_b}{N_0}
Cuanto mayor sea el cociente, quiere decir que el bit tiene mayor energía que el ruido.
Sea una señal, digital o analógica, que contenga datos digitales binarios transmitidos a una determinada velocidad R. Teniendo en cuenta que 1 \, \text{W} = 1 \, \text{J/s}, la energía por bit de la señal será E_b = S \cdot T_b , donde S es la potencia de la señal y T_b es el tiempo necesario para transmitir un bit.
La velocidad de transmisión es R = \frac{1}{T_b}   . Por tanto:
\frac{E_b}{N_0} = \frac{\frac{S}{R}}{N_0} = \frac{S}{kT R}
Nótese que cuando se aumenta la velocidad de transmisión R, la potencia de la señal transmitida S, , debe aumentarse para mantener el cociente \frac{E_b}{N_0} en el nivel deseado.
Para ruido termico Blanco :  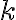N_0 = kT , k = Boltzman’s constant ( N_0 = (1.38 \times 10^{-23}) \cdot T ) y  T = 290 \, \text{K}  para Temp. Ambiente.

Ejercicios Cociente de Energía de Señal por Bit ( \frac{E_b}{N_0} )

Este parámetro tiene relación con la relación señal ruido y por consecuencia con la calidad de señal
y la calidad de los sistemas de comunicaciones digitales.
Se usa para señales digitales o analógicas que contengan datos digitales binarios transmitidos.
Es adecuado para determinar la tasa de error y velocidad de trasmisión.
Retomando:
E_b: Representa la cantidad de energía por bit. Unidad [\text{Joules}]
N_0: El ruido de densidad espectral. Unidad:  [\text{vatios/Hz}] \quad \text{o} \quad [\text{W s}]
Teniendo en cuenta que:
 1 \, \text{vatio} = 1 \, \frac{\text{julio}}{\text{segundo}} \quad \Rightarrow \quad 1 \, \text{julio} = 1 \, \text{vatio} \cdot \text{segundo}
Siendo S la potencia en [vatios] de un bit, y T_b el tiempo que dura un bit [segundos], podemos plantear:
 E_b \, [\text{Joules}] = S \, [\text{vatios}] \cdot T_b \, [\text{segundos}]  (1)
Como T_b es el tiempo de un bit time, la cantidad de Bits por unidad de tiempo se calcula planteando
 \frac{1}{T_b} = C \, [\text{bps ó} \, \frac{1}{\text{s}}] \quad \text{o} \quad C = \frac{1}{T_b} (2)
C resulta ser la Velocidad de transmisión y está expresadas en bits/segundo ó bps. Reemplazando en (1) T_b, tenemos..
 E_b = S \cdot T_b = \frac{S}{C}  (3)
Si planteamos el cociente \frac{E_b}{N_0}:
 \frac{E_b}{N_0} = \frac{\frac{S}{C}}{N_0}  (4)
Si N_0es densidad de potencia del ruido, en vatios por 1 Hz de ancho de banda, podemos expresar  N = kTB
Donde llamamos T a la temperatura absoluta, expresada en Kelvin, B ancho de banda y k es la constante de Boltzman.
Si planteamos el Ruido Térmico por Hz,  N_0 = k \cdot T \quad [\text{W/Hz}] \quad \text{o} \quad [\text{W s}], \quad [\text{J/K}]
Podemos finalmente, plantear la expresión reemplazando N0:
 \frac{E_b}{N_0} = \frac{\frac{S}{R}}{N_0} = \frac{S}{kT C}  (5)
Se lo expresamos en decibeles:
 \left(\frac{E_b}{N_0}\right)_{\text{dB}} = 10 \log\left(\frac{S}{k \cdot T \cdot C}\right) = S_{\text{dBW}} - 10 \log k - 10 \log T \quad  (6) 
\left(\frac{E_b}{N_0}\right)_{\text{dB}} = S_{\text{dBW}} - 10 \log C + 228.6 \, \text{dBW/Hz} - 10 \log T \quad  (7)
También se puede plantear (5) en términos de SNR. Recordando que  N_0 = \frac{N}{B} , con B ancho de banda y densidad espectral de ruido térmico:
 \frac{E_b}{N_0} = \frac{S \cdot B}{N \cdot C}  (8)
Según la fórmula de Shannon, sobre la capacidad de un canal:
 C = B \log_2 \left(1 + \frac{S}{R}\right) \implies \frac{C}{B} = \log_2 \left(1 + \frac{S}{R}\right) \implies 2^{\frac{C}{B}} = 1 + \frac{S}{R} \implies \frac{S}{R} = 2^{\frac{C}{B}} - 1  (9)
Reemplazando (8) en (9)
 \frac{E_b}{N_0} = \frac{B}{C} 2^{\frac{C}{B}} - 1 C: Capacidad [bps], B: Ancho de Banda [Hz].
Esta fórmula es útil por que relaciona la eficiencia espectral (bits por Hz) con la energía de la señal por bit respecto del ruido.
Ejemplo 1
A temperatura ambiente, es decir a  T = 17 \,^{\circ}C \quad \text{o} \quad T = 290 \,K , la densidad de potencia del ruido térmico será:
 N_0 = (1.38 \times 10^{-23}) \times 290 = 4 \times 10^{-21} \, \text{W/Hz} = -204 \, \text{dBW/Hz}
donde dBW corresponde a decibelios-vatio.
Ejemplo 2
En el siguiente ejemplo se relacionan las formulaciones de Shannon y Nyquist. Supóngase que el espectro de un canal está situado entre 3 MHz y 4 MHz y que la \text{SNR}_{\text{dB}} = 24 \, \text{dB} . En este caso,
 B = 4 \, \text{MHz} - 3 \, \text{MHz} = 1 \, \text{MHz}
\text{SNR}_{\text{dB}} = 24 \, \text{dB} = 10 \cdot \log_{10}(\text{SNR})
\text{SNR} = 251
Usando la fórmula de Shannon se tiene que:
 C = 10^6 \cdot \log_2(1 + 251) \approx 10^6 \cdot 8 = 8 \, \text{Mbps}
Éste es un límite teórico difícil de alcanzar. No obstante, supóngase que este límite se puede alcanzar. Según la fórmula de Nyquist, ¿cuántos niveles de señalización se necesitarán? Se tiene que:
 C = 2B \log_2 M
8 \times 10^6 = 2 \times 10^6 \log_2 M
4 = \log_2 M
M = 16
Ejemplo 3
Supongamos que queremos encontrar el máximo \frac{E_b}{N_0} necesario para conseguir una eficiencia espectral de  6 \, \text{bps/Hz} .
 \frac{E_b}{N_0} = \frac{1}{6} \cdot 2^6 - 1 = 10.5 en d_B
10 \cdot \log_{10} 10.5 = 10.21 \, \text{dB}
\frac{E_b}{N_0} = \frac{S \cdot B}{N \cdot C} = \frac{S}{N} \cdot \frac{1}{6}
6 \cdot \frac{E_b}{N_0} = \frac{S}{N}
10 \cdot \log_{10} \left(6 \cdot \frac{E_b}{N_0}\right) = 18 \, \text{dB}
Vamos a tener que lograr en el canal 18 dB para poder transmitir 6 bps por Hz.
Ejemplo 4
Cuál es la capacidad de un canal de “teletipo” de 300 Hz de AB y una S/N de 3 dB. Usando Shannon C = B \cdot \log_2(1 + \frac{S}{R}) \, \text{bps}  pasemos 3 dB a una valor que no esté en decibeles.
 3 \, \text{dB} = 10 \cdot \log_{10} \left(\frac{S}{N}\right) \quad \Rightarrow \quad \frac{S}{N} = 0.5
Entonces:
 C = 300 \cdot \log_2(1 + 0.5) \, \text{bps} = 300 \cdot \frac{\log_{10} 1.5}{\log_{10} 2} \, \text{bps} = 300 \cdot 0.17609 \cdot 0.30102 = 175.48 \, \text{bps}
Ejemplo 5
En la modulación digital binaria PSK (Phase-Shift Keying), para obtener una tasa de error por bit igual a  10^{-4}  (un bit erróneo cada 10.000) se necesita un cociente  \frac{E_b}{N_0} = 8.4 \, \text{dB} . Si la temperatura efectiva es 290 K (temperatura ambiente) y la velocidad de transmisión es 2.400 bps, ¿qué nivel de señal recibida se necesita? 
En este caso se tiene que:
 8.4 = S_{\text{dBW}} - 10 \cdot \log_{10}(2400) + 222.6 \, \text{dBW} - 10 \cdot \log_{10}(290)
8.4 = S_{\text{dBW}} - (10 \cdot 3.38) + 228.6 \, \text{dBW} - (10 \cdot 2.46)
S_{\text{dBW}} = -161.8 \, \text{dBW}