Introducción a Redes
3. Capacidad del Canal
3.2. Capacidad de Canal según SHANNON
La fórmula de Nyquist implica que al duplicar el ancho de banda se duplica la velocidad de transmisión, si todo lo demás se mantiene inalterado. Ahora establezcamos una relación entre la velocidad de transmisión, el ruido y la tasa de errores, esto hace la expresión de Shannon.
La presencia de ruido puede corromper uno o más bits.
Si se aumenta la velocidad de transmisión, el bit se hace más «corto», de tal manera que dado un patrón de ruido, éste afectará a un mayor número de bits. Así pues, dado un nivel de ruido, cuanto mayor es la velocidad de transmisión, mayor es la tasa de errores.
La relación señal-ruido es importante en la transmisión de datos digitales, ya que ésta determi-
na la máxima velocidad de transmisión que se puede conseguir.
Una conclusión de Shannon es que la capacidad máxima del canal, en bits por segundo, verifica la ecuación:
C: Capacidad del Canal
B:Ancho de Banda.
La fórmula de Shannon representa el máximo límite teórico que se puede conseguir.
Si se plantea el límite:
![]()
Como S crece, S/N se hace mucho mayor que 1 y para S muy grande se puede aproximar la expresión a:
Justificación matemática del “límite práctico”
Aunque el modelo matemático dice que C puede aumentar indefinidamente si S aumenta, en la práctica esto no ocurre por dos razones:
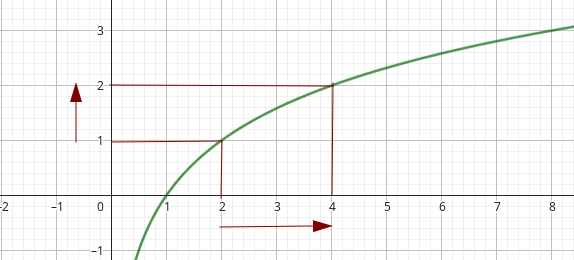
Crecimiento logarítmico: Si quieres duplicar la capacidad, necesitas multiplicar la potencia de señal por un factor grande por el tipo de crecimiento de la función logaritmo, esto implica un costo energético que crece de forma exponencial para pasar en el eje y de 1 a 2 , el eje x debe pasar de 2 a 4 ( duplicar)
Limitaciones físicas: No se puede aumentar S indefinidamente por restricciones de potencia de transmisión, interferencias, radiación no permitida, calentamiento, etc.
Por otro lado el ruido térmico N no se puede reducir a cero ( otra manera de aumentar S/N) ya que N=kTB, donde k es la constante de Boltzmann, T la temperatura absoluta y B el ancho de banda).
La capacidad, tal y como se ha calculado en la fórmula precedente, se denomina capacidad libre de errores.
Como puedo mejorar la capacidad del Canal ?
Que consecuencias puede tener incrementar la potencia de la señal?
Que consecuencias tiene el incrementar el ancho de banda respecto de SNR?


