Sistemas de Control 2

PRIMER PARCIAL

La función de transferencia (FT) de la planta de un grupo motor-generador, donde se vincula la tensión de entrada V_m con la salida de velocidad angular del motor W_m, está dada por la siguiente expresión:

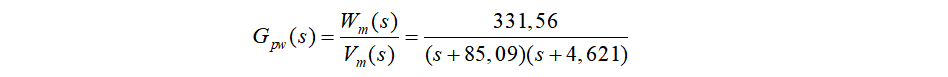
Las características básicas del motor son las siguientes:

La ganancia de normalización para implementación digital en un microcontrolador es K_n = 1/4. La velocidad de regulación del eje del motor es de 1500 RPM o sea, W_ref = 157 rad/s. Con este valor se puede obtener el valor de voltaje de referencia (V_ref) a utilizar dentro del procesador digital.

a) Calcular el valor del ciclo útil (u) a aplicar al modulador PWM para obtener la velocidad de referencia a lazo abierto. Trazar la respuesta al escalón para este ciclo útil mostrando la velocidad en RPM. (0,5 puntos)
Con el objetivo de que para un escalón de V_ref, la respuesta de velocidad en lazo cerrado presente un sobrepaso igual o menor al 2% y un tiempo de asentamiento menor o igual a 0,6 s, se diseña en el dominio del tiempo continuo, un controlador de adelanto de fase con acción integral, cuya función de transferencia resulta:

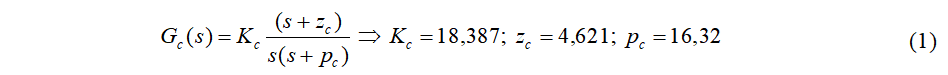
• Primera parte: Rediseño Digital

b) Seleccionar el periodo de muestreo T a partir del tiempo de subida del sistema en lazo cerrado compensado con el controlador indicado en (1), utilizando un número de muestras N_r =10. (0,25 puntos)

c) A partir del método de rediseño digital y con el periodo de muestreo obtenido en el punto anterior, obtener las funciones de transferencia muestreadas del controlador en (1) utilizando las siguientes aproximaciones: 1) Backward; 2) Forward y 3) Invariante al escalón. Presentar sus expresiones en la forma ‘zpk’. (1 punto)

d) Con el periodo de muestreo T, obtener la función de transferencia muestreada de la planta utilizando un ZOH, y, teniendo en cuenta la ganancia del actuador, del sensor y de normalización, obtener con cada uno de los controladores aproximados, lo siguiente, en un mismo gráfico: (2 puntos)
            d.1) las respuestas al escalón de velocidad del sistema en LC para el valor de V_ref junto con la respuesta de velocidad en tiempo continuo utilizando el compensador (1).
            d.2) las respuestas al escalón de la acción de control en LC para el valor de V_ref junto con la respuesta de acción de control en tiempo continuo utilizando el compensador (1).
OBSERVACIONES: En cada figura tienen que aparecer 4 curvas; 1 del sistema en tiempo continuo y 3 del sistema en tiempo discreto.

e) Indicar en el texto (no en las figuras), los valores de sobrepaso y de tiempo de asentamiento de las respuestas de velocidad y el pico máximo y el valor de régimen permanente para las respuestas de las acciones de control, para cada caso. (0,5 puntos)

f) A partir de la información suministrada en el punto ‘e’ y observando las gráficas proponga las soluciones que considere adecuadas para mejorar el régimen transitorio, y elija la aproximación que utilizaría justificando su respuesta. Por otro lado, razonar ¿porque no se agrega un atraso en las respuestas obtenidas debido a la implementación digital? (0,5 puntos)

g) Observando los coeficientes de las funciones de transferencia de los controladores en tiempo discreto obtenidos en el punto c, los valores máximos alcanzados por la variable controlada y la acción de control en cada caso, indicar ¿qué formato Q utilizaría si tiene que emplear un microcontrolador con tamaño de palabra de 16 bits y aritmética de punto fijo? (1 punto)

h) Indicar para el rediseño digital realizado, cuál es el valor de la frecuencia de Nyquist. (0,25 puntos)

i) Obteniendo la FT en tiempo discreto del compensador en (1) utilizando Tustin, agregue la compensación del ZOH con el escalar e = 0. Trace la respuesta al escalón de la velocidad y de la acción de control para V_ref. Escriba las conclusiones sobre las mejoras obtenidas. (0,5 puntos)

j) Obtener la ecuación recursiva a diferencias finitas del compensador final con la compensación del ZOH y describa ¿Qué formato de punto fijo utilizaría si tiene que implementar el control en un microcontrolador con tamaño de palabra de 32 bits y aritmética de punto fijo? (1 punto)

• Segunda parte: Diseño en el tiempo discreto

k) Debido a cambios de carga periódicas en la salida del generador y poder mantener el desempeño transitorio conseguido, se debe aumentar la frecuencia de muestreo. Obtener el periodo de muestreo empleando la relación: ω_m = 60×BW_scc, siendo ω_m la frecuencia angular de muestreo y BW_scc el ancho de banda del sistema con compensador en tiempo continuo. (0,25 puntos)

l) En base a la nueva frecuencia de muestreo obtenida responda ¿cuál es la máxima frecuencia que el sistema de control en tiempo discreto puede compensar? (0,25 puntos)

m) Obtener la planta muestreada para el nuevo periodo utilizando un ZOH, teniendo en cuenta el atraso de un periodo de muestreo por la implementación digital. Diseñar la misma estructura de compensación planteada para tiempo continuo dada por la siguiente función de transferencia:

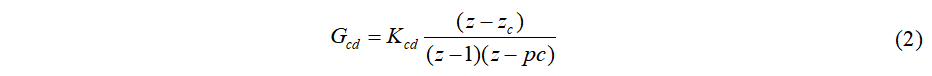
Definir el cero del compensador, cancelando el polo dominante de la planta en tiempo discreto obtenida en el punto anterior, y, mediante el método del LGR en el plano z, para las mismas especificaciones de desempeño iniciales, diseñar el polo y la ganancia del compensador. (1 punto)

n) Trazar la respuesta al escalón de V_ref de la velocidad y de la acción de control. Si es necesario, realizar un ajuste para que la acción de control no supere la unidad. (0,5 puntos)

o) Trazar el diagrama de Bode para verificar los márgenes de estabilidad y compararlo con el Bode del sistema compensado en tiempo continuo. Analice ambos casos, y, en base a las diferencias que observe, obtenga las conclusiones correspondientes. (0,5 puntos)