5. Representación binaria de decimales

5.1. Complemento a dos

La forma indicada posee dos variantes para la representación de los números enteros: “Signo-Magnitud” y “Complemento a 2”, siendo esta última la utilizada por los dispositivos digitales que poseen capacidad para efectuar operaciones aritméticas.

En la representación binaria de “Signo-Magnitud”, el bit de signo permite representar a números positivos y negativos de acuerdo a lo siguiente:

  • S = 0; número entero positivo.
  • S = 1; número entero negativo.

La magnitud (o valor absoluto) del número es representada directamente en binario puro.

Ejemplo A2=10111  B2=01100.

  • Para A2 :  1 0111  =  – 7
  • Para B2 :  0 1100  =  + 12

Complemento a dos

Otra forma de representar a los números binarios enteros es en “complemento a 2”. En esta representación, los números positivos son expresados como si estuvieran en “Signo-Magnitud”, mientras que los números negativos se cambia a complemento a 2.

Como es el complemento a dos?

El complemento a 2 de un número binario se obtiene en dos pasos:

  1. invirtiendo bit a bit el número (a esto se denomina complemento a 1) 
  2.  sumándole “1”. 

Nota: cabe aclarar que en la representación de complemento a 2 el MSB (Bit Mas Significatido) siempre es el bit de signo y su representación es igual que en “Signo-Magnitud”. 

El siguiente ejemplo muestra cómo obtener el complemento a 2.

Ejemplo 1 :Representar Complemento a dos A2=10110

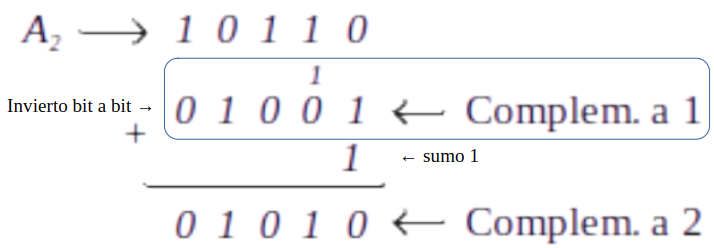
En este ejemplo el bit de signo de A es 1, por lo tanto es un número negativo. Si complementamos a 2 obtenemos (como se muestra en la imagen)  obtenemos la magnitud de A, el complemento a 2 de este número es 01010  que sería el 1010 , por lo tanto A2=10110 es -1010.

Ejemplo 2 :Representar Complemento a dos B2=01100



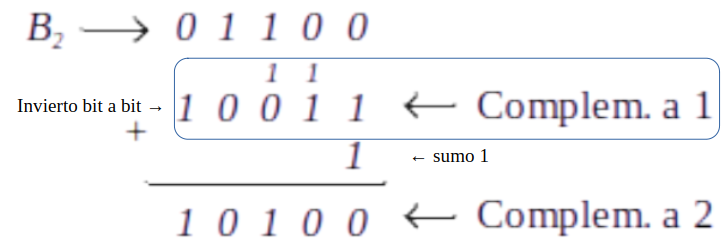
En este caso el bit de signo de B es 0, por lo tanto es un número positivo. En este caso, se tiene B10= +12 (011002) y su opuesto será B2= 101002(–12).

Podemos ver que de manera sencilla el complemento a dos permite cambiar de una representación binaria negativa a positiva.


Por que se suma 1 en el complemento a 2?

Vimos que la receta para calcular el complemento a 2 es:
  1. invirtiendo bit a bit el número (a esto se denomina complemento a 1) 
  2.  sumándole “1”. 
Queda preguntarse por que simplemente no usamos la regla 1 ( complemento a 1) en el cálculo?. Veamos que pasaría.

Si solo cambiamos, invertimos el bit a bit (complemento a 1) el cero quedaría: 11111 ó 00000

Esto provoca que haya dos representaciones del cero:

  • 00000000 = +0

  • 11111111 = -0 (problema ❌)

Veamos un ejemplo del problema con 4 bits.
  • +3  =  0011
  • -3  =  1100  (Complemento a 1)
  • +0  =  0000
  • -0  =  1111  ❌ (problema)
Tener -0 (1111)  y 0 (0000),  causa ambigüedades y requiere lógica adicional en el hardware para tratar ambos valores como iguales.

Con el complemento a 2, se soluciona el problema del doble cero cambiando la forma de representar los números negativos, se invierten los bits (como en complemento a 1), se suma 1 al resultado para obtener el negativo.

Beneficios del uso de Complemento a dos.

1. La suma y resta se realizan de la misma manera que en números sin signo.
2. No hay dos representaciones del cero.
3. El bit más significativo actúa como un indicador de signo.
4. La resta se convierte en suma.
5. Simplicidad en comparación de números.Se pueden comparar números directamente con las operaciones lógicas de la CPU.Como los números negativos en complemento a 2 son mayores que los positivos en términos de orden binario, las comparaciones (>, <) funcionan sin necesidad de ajustes adicionales.
6. Manejo natural del desbordamiento. Es fácil detectar desbordamiento (overflow).
En complemento a 2, si dos números del mismo signo se suman y el resultado cambia de signo inesperadamente, ha ocurrido un desbordamiento.

Conclusión: ¿Por qué Complemento a 2 es el estándar?

✔ Suma y resta funcionan igual que en binario normal.
✔ No hay dos representaciones para el cero.
✔ El bit más significativo indica el signo directamente.
✔ La resta se convierte en suma, reduciendo la complejidad del hardware.
✔ El desbordamiento es fácil de detectar.
✔ Las comparaciones funcionan sin lógica extra.



hasta Página 8 del apunte de Guillermo