Análisis Numéricos.
2. Método de Newton Raphson
2.1. Código Fuente
//Autor Desconocido
#include <iostream>
using namespace std;
//Seccion de #includes
#include <iostream>
#include <iomanip> // setprecision
#include <cmath>
//Seccion constantes simbolicas
#define PRECISION 10 //Cantidad maxima de decimales
#define MAX_ITERACIONES 100 //Cantidad maxima de iteraciones
#define INTERVALOS 6 //Intervalos posibles
//Prototipos
void tabula(double a, double b, int intervalos); // Muestra un # tabulado de intervalos
double f(double x); // Retorna el valor de la funcion evaluada en x
double f_derivada(double x); // Retorna la derivada de la funcion evaluada en x
int main()
{
double a;
double b;
double tolerancia; // Tolerancia
double x0; // Primera aproximacion
double x1; // Siguiente aproximacion
double error; // Diferencia entre dos aproximaciones sucesivas: x1 - x0
int iteracion; // # de iteraciones
bool converge = true;
cout << setprecision(PRECISION); // Se establece la precision
cout << "\nCalculo de las raices de una funcion aplicando el metodo de Newton - Raphson\n";
cout << "\nIngrese el intervalo inicial [a,b]:" << endl;
// Se ingresa el intervalo
cout << "\na = ";
cin >> a;
cout << "b = ";
cin >> b;
// Se tabulan los valores de f para INTERVALOS intervalos
tabula(a, b, INTERVALOS);
// Se pide elegir una aproximaci�n inicial
cout << "\nEscoja el punto inicial adecuado: x0 = ";
cin >> x0;
// Se pide ingresar la tolerancia
cout << "Tolerancia = ";
cin >> tolerancia;
// Iteraciones
// Se imprimen los valores de la primera aproximacion
cout << "\nAproximacion inicial:\n";
cout << "x0 = " << x0 << "\n"
<< "f(x0) = " << f(x0) << "\n"
<< "f'(x0) = " << f_derivada(x0) << endl;
iteracion = 1;
do {
if (iteracion > MAX_ITERACIONES) {
converge = false; // Se sobrepas� la m�xima cantidad de iteraciones permitidas
break;
} else {
x1 = x0 - f(x0) / f_derivada(x0); // C�lculo de la siguiente aproximaci�n
error = fabs(x1 - x0); // El error es la diferencia entre dos aproximaciones sucesivas
// Se imprimen los valores de la siguiente aproximaci�n x1, f(x1), f_derivada(x1), error
cout << "\nIteracion #" << iteracion << endl;
cout << "x" << iteracion << " = " << x1 << "\n"
<< "f(x" << iteracion << ") = " << f(x1) << "\n"
<< "f'(x" << iteracion << ") = " << f_derivada(x1) << "\n"
<< "error = " << error << endl;
// La diferencia entre dos aproximaciones sucesivas es tambi�n conocida como error.
// La condici�n de terminaci�n consiste en que que el error debe ser <= que la tolerancia dada
// Si se cumple la condici�n de terminaci�n, se ha encontrado la raiz aproximada buscada.
if (error <= tolerancia) { // Condici�n de terminaci�n
converge = true;
break;
// Si no se cumple el criterio de terminaci�n, se pasa a la siguiente iteraci�n
} else {
x0 = x1;
iteracion++;
}
}
} while (1);
// Respuesta final
if (converge) {
cout << "\n\nPara una tolerancia de " << tolerancia << " la raiz de f es: " << x1 << endl;
} else {
cout << "\n\nSe sobrepas� la m�xima cantidad de iteraciones permitidas" << endl;
}
cin.get();
cin.get();
return 0;
}
void tabula(double a, double b, int intervalos)
{
int puntos = intervalos + 1;
double ancho = (b - a) / intervalos;
cout << "\n\tx\t\tf(x) " << endl;
for (int i = 0; i < puntos; i++) {
cout << "\t" << a << "\t\t" << f(a) << endl;
a = a + ancho;
}
}
//Esta es la funci�n de nuestro ejemplo
double f(double x)
{
return x * exp(cos(x)) / 1.5 - 1;
//return exp(-x) + 3 * x - 3;
}
//Esta es la derivada de la funci�n de nuestro ejemplo
double f_derivada(double x)
{
return exp(cos(x)) * (1 - x * sin(x)) / 1.5;
//return -1 * exp(-x) + 3;
}
De observar la gráfica en los entornos cercanos al origen de eje x e y vemos que x1=2 e x2=4 son puntos en los que se observa que la curva tiene una raíz ( y=0) . La ejecución de esto se vería:
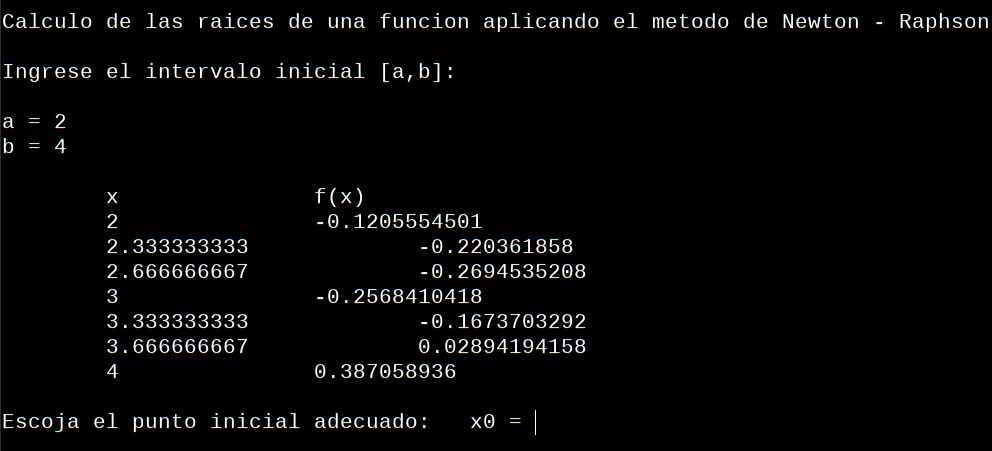
Podemos ver los cambios de signos en los distintos valores de f(x), esto nos dá una pista de los valores de x que podemos proponer para iniciar otra iteración con puntos cercanos a la raiz.

Vamos a tomar 3.3 como inicio para un nuevo cálculo, la salida sería:

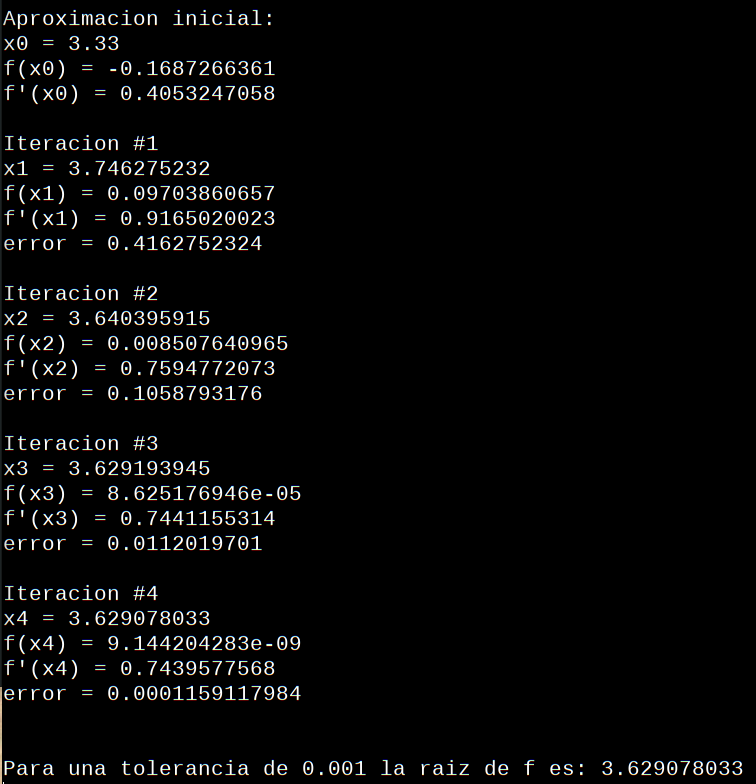
Lo que se indica como error en la iteración, es la diferencia respecto del cálculo anterior. Vamos a probar con otros valores que permitan realizar mas iteraciones. Vemos que hay otra raiz entre 0 y 1 coma algo...
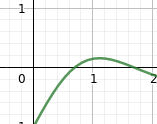
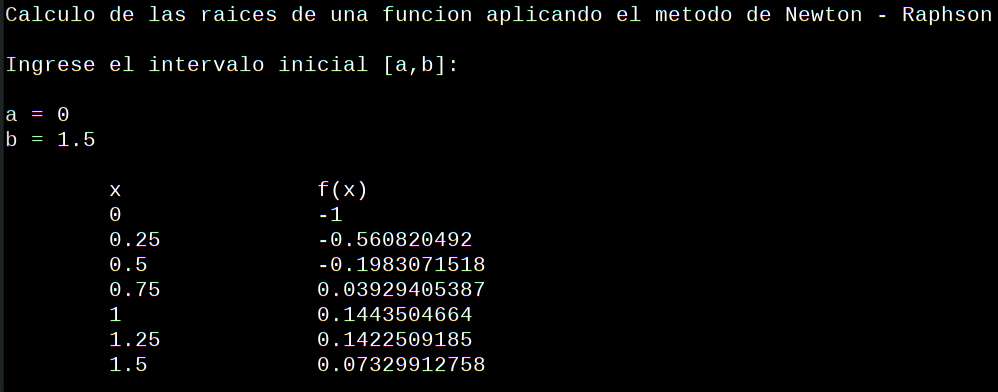
Nuevamente podemos ver que los signos de f(x) cambian para x1= 0.5 y x2=0.75 , así que ponemos como punto de inicio, 0.5 y elegimos una precisión de 0.01
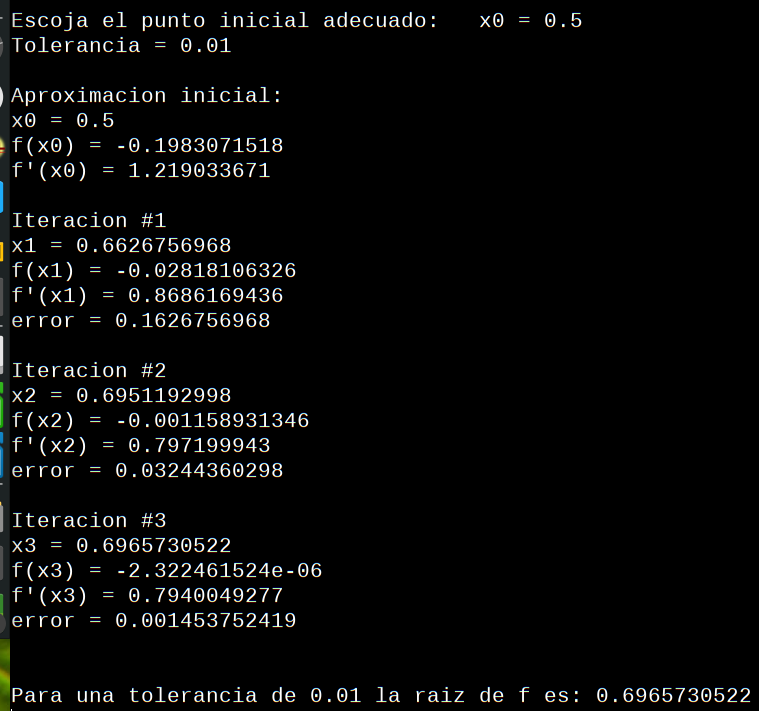
En este caso luego de 3 iteraciones se obtiene la tolerancia deseada.